读书笔记-函数式编程指北

Posted on Edited on In

《函数式编程指北》读书笔记
中文版

函数是一等公民

和其他对象一样，可以像对待任何其他数据类型一样对待它们——把它们存在数组里，当作参数传递，赋值给变量…等等

非常小心 this 值，特别是以一等公民的方式调用 this…

纯函数

相同的输入，永远会得到相同的输出，而且没有任何可观察的副作用

纯函数不依赖外部环境，从而降低了认知负荷；函数能够做到自给自足。更可以用 Object.freeze 把对象变成不可变的，从而保留纯粹性，因为状态不会有变化

副作用是计算结果的过程中，系统状态的一种变化，或者与外部世界进行的可观察的交互

函数式编程的哲学就是假定副作用是造成不正当行为的主要原因

纯函数的优点：

  • 可缓存性（Cacheable）：总能够根据输入来做缓存，一种典型方式是 memoize 技术
  • 可移植性/自文档化（Portable/Self-Documenting）：依赖明确（所有的依赖都需用函数的参数传递），纯函数对其依赖必须要诚实，并且参数化能够使应用更加灵活，与环境无关
  • 可测试性（Testable）：只需要简单地给函数一个输入，然后断言输出就好了
  • 合理性（Reasonable）：引用透明性（referential transparency，即如果一段代码可以替换成它执行所得的结果，而且是在不改变整个程序行为的前提下替换的）
  • 并行代码：因为纯函数根本不需要访问共享的内存，也不会因副作用而进入竞争态，所以我们可以并行运行任意纯函数

可以通过延迟执行的方式把不纯的函数转换为纯函数

柯里化

只传递给函数一部分参数来调用它，让它返回一个函数去处理剩下的参数

lodash 的 curry 方法

1
2
3
4
_.curry(func, [arity=func.length])
// 创建一个函数，该函数接受 func 的参数
// 如果全部参数已经提供，则直接返回 func 执行的结果
// 否则返回一个函数，接受余下的参数

对于传进去的 func 的参数，需要把要操作的数据放到最后一个参数

表明了一种“预加载”函数的能力，通过传递一到两个参数调用函数，就能得到一个记住了这些参数的新函数

只传给函数一部分参数通常也叫作局部调用，能够大量减少样板文件代码

curry 函数是纯函数

代码组合

compose：将两个函数结合起来，得到一个新函数

1
2
3
4
5
var compose = function(f, g) {
    return function(x) {
        return f(g(x));
    }
}

g 先于 f 执行，从右向左的数据流

结合律

如何为 compose 的调用分组不重要，结果是一样的

1
var associative = compose(f, compose(g, h)) == compose(compose(f, g), h); // true

因此，可以给 compose 传递很多参数而不必自己手动分组，它自己会决定如何分组（这个时候 compose 就不是上面写的那个只接受两个参数的了，而要写个多个的）

因为有了结合律，所以任何一个函数分组都可以被拆开来，然后再以它们自己的组合方式打包在一起

如何组合的最佳实践：让组合可重用

pointfree

函数无须提及将要操作的数据是什么样的

1
2
3
4
5
6
7
// 非 pointfree，因为提到了数据：word
var snakeCase = function (word) {
  return word.toLowerCase().replace(/\s+/ig, '_');
};

// pointfree
var snakeCase = compose(replace(/\s+/ig, '_'), toLowerCase);

一等公民的函数+柯里化+组合协作起来，通过管道把数据在接受单个参数的函数间传递

pointfree 模式能够帮助我们减少不必要的命名，让代码保持简洁和通用

在组合时注意如果想组合类似 map 这种接受两个参数的函数，需要先对 map 局部调用使得其返回接受一个参数的函数

在 debug 过程中可以用 trace 函数来追踪代码执行情况，在想要观察的特定点（管道的某一环）观察数据

范畴学

把很多数学分支（集合论、类型论、群论、逻辑学等…）中相同的概念加以形式化

…范畴：有以下这些组件（component）的搜集（collection）就构成了一个范畴

  • 对象的搜集
  • 态射的搜集
  • 态射的组合
  • indentity 这个独特的态射

对应到编程上：

  • 对象的搜集：数据类型，例如 String Boolean Number Object 等。通常我们把数据类型视作所有可能的值得一个集合，这样可以用集合论处理类型

  • 态射的搜集：态射是标准的、普通的纯函数

  • 态射的组合：本章介绍的组合 compose。在范畴学中任何组合都适用结合律

  • indentity 这个独特的态射

    1
    var id = function(x) { return x; };

    有了 id 函数，就可以有单位律（和实数的单位元一样）

    1
    compose(id, f) = compose(f, id) == f;

示例应用

声明式代码：指明“做什么“，而不是”怎么做“

命令式 声明式
for 循环，硬编码处理迭代累加blabla… map
硬编码顺序调用函数 compose 组合函数，不指定执行顺序（天然地适合并行运算），为潜在的代码更新提供支持

map 的组合律

1
var law = compose(map(f), map(g)) == map(compose(f, g));

可以用来重构代码（就像数学推导公式一样）

类型签名

Hindley-Milner 系统

函数写成 a -> b 的样子，表示接受值和返回值

连续指向

1
2
3
4
// map :: (a -> b) -> [a] -> [b]
var map = curry(function(f, xs) {
    return xs.map(f);
});

最简单的理解：map 接受两个参数，第一个是 f，类型为 a -> b；第二个是 xs，类型为 [a]；返回一个数组 [b]

深入理解：从右向左加括号 (a -> b) -> ([a] -> [b])，外层是输入一个 a -> b 返回 [a] -> [b]，输入一个函数返回一个函数；内层是 [a] -> [b]，输入数组返回数组

仅仅根据类型签名，就可以理解函数做了什么事情，比如 map 其实就是在每个 a 上调用一次 f(a -> b)，从而得到一个 [b]

另一个例子

1
2
3
4
// reduce :: (b -> a -> b) -> b -> [a] -> b
var reduce = curry(function(f, x, xs) {
    return xs.reduce(f, x);
})

理解：

  • 第一个参数f：(b -> a -> b)，接受一个 b 一个 a，返回 b
  • 那么这里的 a b 来源于哪里呢，其实就在第二三个参数 b 和 [a]，这里的 b a 会传给 f 作为参数
  • reduce 的最终返回结果是一个 b，其实就是 f :: b -> a -> b 的这个输出 b
  • 对照 reduce 的真实定义 来理解：
    • f 即要对数组中每个值执行的函数，它的参数实际上是：b 为 accumulator 即累计回调的值，a 为 currentValue 即正在处理的当前数组元素
    • x 是第一次调用 f 时的初始值
    • xs 是数组，不用讲了…

Parametricity

wiki （暂时还没理解这个概念啥意思）

但反正这个特性表明，函数将会以一种统一的行为作用于所有的类型

也就是说，在看着类型签名进行函数功能的推断时，要保证函数对每一个可能的类型操作必须保持统一，这样就能缩小可能的功能的范围

例如，// head :: [a] -> a，a 可能是任意类型，所以函数在对 a 一无所知的情况下，可能对 [a] 进行的操作，只可能是返回数组中的某个元素

自由定理

根据（多态）类型签名，可以无需知道函数具体实现的情况就对函数表达式进行推导得到一些普适的重写规则，从而可以重构代码，提高代码效率

类型约束

也可以把类型约束为一个特定的接口（interface）

容器

Indentity

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var Container = function(x) {
    // 装载任意类型的值
    this.__value = x;
}

// 构造器
Container.of = function(x) { 
    return new Container(x); 
};
// 一个让别的函数（f）能操作容器中值的方法
// 这样就可以不离开 Container 而操作容器里面的值
// 可以 Container.of(2).map(blabla).map(blabla) 连续调用
// 啊哈，那 map 就是个组合（compostion）了
Container.prototype.map = function(f) {
    return Contain.of(f(this.__value));
}

functor：实现了 map 函数并遵守一些特定规则的容器类型

把值装进一个容器，而且只能使用 map 来处理它——是抽象，对函数运用的抽象（当 map 一个函数的时候，我们请求容器来运行这个函数）

Maybe

另一种 functor：处理空值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
var Maybe = function(x) {
    this.__value = x;
};
Maybe.of = function(x) {
    return new Maybe(x);
};
Maybe.prototype.isNothing = function() {
    return (this.__value === null || this.__value === undefined);
};
Maybe.prototype.map = function(f) {
    return this.isNothing()
        ? Maybe.of(null)
    	: Maybe.of(f(this.__value));
};

这样我们在使用 map 时代码就不会报错了，而是会得到 Maybe(null)

Maybe 最常用在那些可能会无法成功返回结果的函数中，通过（人工或自动）抛出 Maybe(null) 可以实现失败时立即切断执行

more pointfree…

any_functor_at_all 即为我们上面创建的 Contianer、Maybe 等任意 functor，这样就把 functor 的点记式 map 代理成了 pointfree 的 map 了

1
2
3
4
// map :: Functor f => (a -> b) -> f a -> f b
var map = curry(function(f, any_functor_at_all) {
    return any_functor_at_all.map(f);
});

一个帮助函数 maybe，用于返回一个自定义的值然后还能继续执行后面的代码

1
2
3
4
// maybe :: b -> (a -> b) -> Maybe a -> b
var maybe = curry(function(x, f, m) {
    return m.isNothing() ? x : f(m.__value);
});

Either

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
var Left = function(x) {
    this.__value = x;
};
Left.of = function(x) {
    return new Left(x);
};
Left.prototype.map = function(f) {
    return this;
};

var Right = function(x) {
    this.__value = x;
};
Right.of = function(x) {
    return new Right(x);
};
Right.prototype.map = function(f) {
    return Right.of(f(this.__value));
};
1
2
3
4
5
Right.of('rain').map(function(str){ return 'b'+str; });
// Right('brain')

Left.of('rain').map(function(str){ return 'b'+str; });
// Left('rain') !here

Right 就像个 Container，而 Left 无视了我们的 map 请求

Left 可以用来返回错误，让程序短路，比 Maybe(null) 好的是，我们可以在可能错误的地方给 Left 传错误信息了

Left 和 Right 是 Either 抽象类型的两个子类，一个（伪）类型签名可以这样写：

1
2
3
// Either(String, Number)
// String 表示左边的值是 String，也就是 Left(String)
// Number 表示右边 Right(Number)

lift：一个函数在调用的时候，如果被 map 包裹了，那么它就会从一个非 functor 函数转换为一个 functor 函数，我们把这个过程叫做 lift。一个比较好的实践是，仍按照普通方式去写（操作普通数据类型的）函数，在必要的时候再通过 lift 变为合适的容器去操作容器类型，这样能得到更简单、重用性更高的函数，它们能够随需求而变，兼容任意 functor

帮助函数 either

1
2
3
4
5
6
7
// either :: (a -> c) -> (b -> c) -> Either a b -> c
var either = curry(function(f, g, e) {
    switch(e.constructor) {
        case Left: return f(e.__value);
        case Right: return g(e.__value);
    }
})

IO

1
2
3
4
5
6
7
8
9
10
11
var IO = function(f) {
    this.__value = f;
};
IO.of = function(x) {
    return new IO(function() {
        return x;
    });
};
IO.prototype.map = function(f) {
    return new IO(_.compose(f, this.__value));
};

IO 把非纯动作捕获到包裹函数里，目的是延迟这个非纯动作。我们可以认为 IO 包含的是被包裹的执行动作的返回值，而不是包裹函数本身（在 of 函数中可以看出，IO(function() { return x; }) 仅仅是为了延迟执行，其实我们得到的是 IO(x)

通过链式调用 map，其实是把传给 map 的函数们压入一个“运行栈”，直到最终调用者调用时才会运行这些（不纯的）函数们

异步任务

Task

一点理论

1
2
3
4
5
// identity 同一律
map(id) === id;

// composition 组合律
compose(map(f), map(g)) === map(compose(f, g));

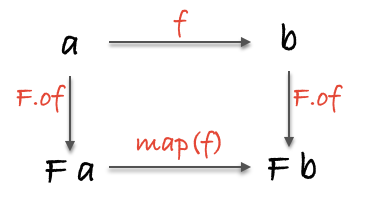
在范畴学中，functor 接受一个范畴的对象和态射（morphism），然后把它们映射（map）到另一个范畴里去

可以把范畴想象成一个有着多个对象的网络，对象之间靠态射连接。那么 functor 可以把一个范畴映射到另外一个，而且不会破坏原有的网络

functor diagram

Monad

pointed functor

pointed functor 是实现了 of 方法的 functor

关键是用 of 把任意值丢到容器里然后就可以开始到处使用 map 的能力，像这样：

1
any_pointed_functor.of(any_value).map(f)

of 方法不是用来避免 new 关键字的，而是用来把值放到默认最小化上下文（default minimal context）中的（我们希望容器类型的任意值都能发生 lift，然后像所有的 functor 那样再 map 出去）

monad

monad 是可以变扁（flatten）的 pointed functor

因为在连续的 functor 传递中，值会被包成 functor(value) -> 传给下一个函数 -> 而下一个函数是普通函数需要用 map 包一下以处理 functor -> 处理完就变成了 functor(functor(value)) -> 那么再下一个函数就需要包两层 map…

例如，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//  safeProp :: Key -> {Key: a} -> Maybe a
var safeProp = curry(function(x, obj) {
  return new Maybe(obj[x]);
});

//  safeHead :: [a] -> Maybe a
var safeHead = safeProp(0);

//  firstAddressStreet :: User -> Maybe (Maybe (Maybe Street) )
var firstAddressStreet = compose(
  map(map(safeProp('street'))), map(safeHead), safeProp('addresses')
);

firstAddressStreet(
  {addresses: [{street: {name: 'Mulburry', number: 8402}, postcode: "WC2N" }]}
);
// Maybe(Maybe(Maybe({name: 'Mulburry', number: 8402})))

为了解决这个一层一层洋葱一样的嵌套，可以在 functor 上定义一个 join 方法，这个 functor 就成为了一个 monad

1
2
3
4
5
6
7
8
Maybe.prototype.join = function() {
    return this.isNothing() ? Maybe.of(null) : this.__value;
}

var mmo = Maybe.of(Maybe.of('nunchuncks'));
// Maybe.of(Maybe.of('nunchuncks'))
mmo.join();
// Maybe.of('nunchuncks') -> flatten!!

用 monad 魔法改造上面的 firstAddressStreet 例子，在每次得到嵌套 Maybe 后加一个 join 把它变平

1
2
3
4
5
6
7
8
9
10
11
//  join :: Monad m => m (m a) -> m a
var join = function(mma) { return mma.join(); };

//  firstAddressStreet :: User -> Maybe Street
var firstAddressStreet = compose(join, map(safeProp('street')), join, map(safeHead), safeProp('addresses')
);

firstAddressStreet(
  {addresses: [{street: {name: 'Mulburry', number: 8402}, postcode: "WC2N" }]}
);
// Maybe({name: 'Mulburry', number: 8402})

chain

上面的例子中包含一种模式：我们总是在紧跟着 map 的后面调用 join。我们可以把这个行为抽象到一个叫做 chain 的函数中

1
2
3
4
//  chain :: Monad m => (a -> m b) -> m a -> m b
var chain = curry(function(f, m) {
    return m.map(f).join(); // or compose(join, map(f))(m)
});

chain 也叫作 >>= （读作 bind）或者 flatMap，重构一下上面的例子

1
2
3
4
5
6
7
// map/join
var firstAddressStreet = compose(join, map(safeProp('street')), join, map(safeHead), safeProp('addresses')
);

// chain
var firstAddressStreet = compose(chain(safeProp('street')), chain(safeHead), safeProp('addresses')
);

因为 chain 可以轻松嵌套多个作用，因此我们就能以一种纯函数式的方式来表示 序列（sequence）和 变量赋值（variable assignment）。像这样：

1
2
Maybe.of(null).chain(safeProp('address')).chain(safeProp('street'));
// Maybe(null)

使用插入式的 chain，避免了 compose 时还需要几个帮助函数

记住：返回的如果是“普通”值就用 map，如果是 functor 就用 chain

理论

1
2
// 结合律
compose(join, map(join)) == compose(join, join)

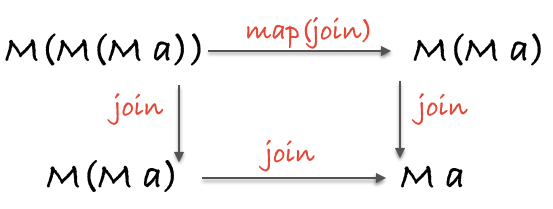
monad associativity law

1
2
// 三角同一律
compose(join, of) == compose(join, map(of)) == id

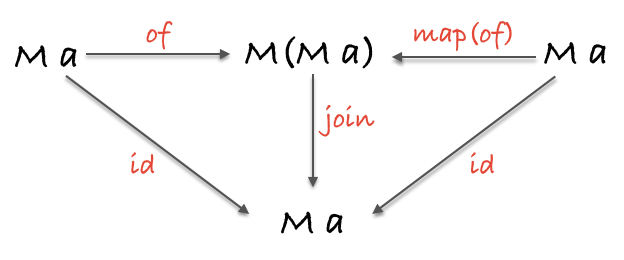
monad identity law

Applicative Functor

ap 就是这样一种函数，能够把一个 functor 的函数值应用到另一个 functor 的值上。

比如我们想让两个 Container 的值相加，

1
2
3
4
5
6
7
8
9
10
11
// 这样是行不通的, 因为 2 和 3 都藏在 Container 里
add(Container.of(2), Container.of(3));
// NaN

// 使用可靠的 map 函数, 得到一个局部调用的 add(2)
var container_of_add_2 = map(add, Container.of(2));
// Container(add(2))

Container.of(2).chain(function(two) {
    return Container.of(3).map(add(two));
})

ap 版本

1
2
3
4
5
6
7
8
Container.prototype.ap = function(other_container) {
    return other_container.map(this.__value);
    // this.__value 是一个函数, 接受另一个 functor 作为参数
};

// 这样使用
Container.of(add(2)).ap(Container.of(3)); // Container(5)
Container.of(2).map(add).ap(Container.of(3)); // Container(5)

applicative functor 是实现了 ap 方法的 pointed functor

一个特性：map 一个 f 等价于 ap 一个值为 f 的 functor

1
F.of(x).map(f) == F.of(f).ap(F.of(x))

applicative functor 可以使几个（独立的不需要依赖顺序的）函数同时执行

1
2
3
4
5
6
// Http.get :: String -> Task Error HTML
var renderPage = curry(function(destions, events) { /* render page */ });
Task.of(renderPage).ap(Http.get('/destinations')).ap(Http.get('/events'))
// 两个 HTTP 请求会同时执行，当两者的响应都返回之后 renderPage 才会被调用
// 是使用局部调用的函数来达成上述结果的，所以必须保证 renderPage 是 curry 函数（没想明白！）
// 调用了两次 ap，每次调用中 renderPage 就收到一个参数然后运行，直到所有的参数都传进来它也就执行完毕了

lift

1
2
3
4
5
6
7
var liftA2 = curry(function(f, functor1, functor2) {
    return functor1.map(f).ap(functor2);
});
var liftA3 = curry(function(f, functor1, functor2, functor3) {
    return functor1.map(f).ap(functor2).ap(functor3);
})
// liftA4, etc...

让那些小代码块发生 lift，成为 applicative functor 中的一员

一个实际用例：

1
2
3
4
5
6
7
8
9
// checkEmail :: User -> Either String Email
// checkName :: User -> Either String String

// createUser :: Email -> String -> IO User
ver createUser = curry(function(email, name) { /* creating */ });

Either.of(createUser).ap(checkEmail(user)).ap(checkName(user));

liftA2(createUser, checkEmail(user), checkName(user));

衍生函数

of/ap = map

1
2
3
X.prototype.map = function(f) {
    return this.constructor.of(f).ap(this);
}

chain -> functor applicative（但会失去 ap 并行的能力）

1
2
3
4
5
6
7
8
9
10
11
12
X.prototype.map = function(f) {
    var m = this;
    return m.chain(function(a) {
        return m.constructor.of(f(a));
    });
}

X.prototype.ap = function(other) {
    return this.chain(function(f) {
        return other.map(f);
    })
}

定律

  • applicative functor 是组合关闭（closed under composition）的，意味着 ap 永远不会改变容器类型

  • 同一律（identity）

    1
    2
    A.of(id).ap(v) == v
    map(id) == id

  • 同态（homomorphism）

    1
    A.of(f).ap(A.of(x)) == A.of(f(x))

    同态就是一个能够保持结构的映射，实际上，functor 就是一个在不同范畴间的同态，因为 functor 在经过映射之后保持了原始范畴的结构

  • 互换（interchange）

    1
    v.ap(A.of(x)) == A.of(function(f) { return f(x) }).ap(v)

  • 组合（composition）

    1
    A.of(compose).ap(u).ap(v).ap(w) == u.ap(v.ap(w));